https://www.acmicpc.net/problem/3020
3020번: 개똥벌레
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이
www.acmicpc.net
1. 풀이 방법
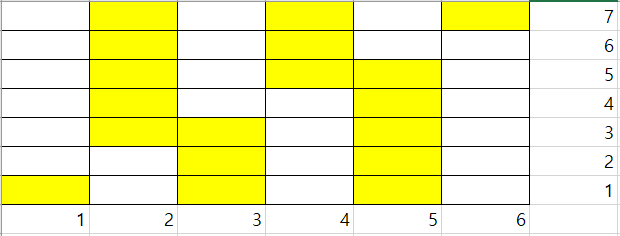
문제에 주어진 예제1번을 그려보면 이렇게 된다.
편하게 생각할려고 세로축을 밑에서부터 1로 생각했다.

석순(인덱스가 홀수(odd)), 종유석(인덱스가 짝수(even))를 나누어서 계산했다.
생각해보면 높이가 1일 때, 1과 같거나 큰수에서 부딪힌다는 것을 알 수 있다.
따라서 만약 내가 높이 1일때 몇개의 석순에 부딪히는지 알고 싶다면, 1보다 크거나 같은 석순의 개수를 세어주면 된다.
그래서 계수정렬을 하는 것 처럼 1~N까지의 개수를 각각 세주었다.

odd배열과 even배열 모두 1이 1개, 3이 1개, 5가 1개인 것을 알 수 있다.

이때, 숫자 개수의 누적합을 구하면 [1,1,2,2,3,3] 과 같은 결과가 나온다.
이 뜻은 높이가 1일때, 1보다 작거나 같은 석순이 1개
높이가 2일때, 2보다 작거나 같은 석순이 1개
높이가 3일때, 3보다 작거나 같은 석순이 2개 있다는 뜻이다.
따라서 h(구하고 싶은 높이)가 1~H인 for문을 돌면서 해당 누적합을 이용하면 몇개의 장애물을 파괴해야 하는지 알 수 있다.
이때 누적합을 이용하는 방법은 odd[H]-odd[h-1] 이다. 왜냐하면 h<= 구간합 <=H 가 h보다 크거나 같은 석순의 누적합이기 때문이다.
반대로 종유석(even)을 구하기 위해서는 배열을 생각하는게 편하다.

원래는 밑에서부터 index가 1이였지만, 지금은 위에서부터 1~7로 생각해보자.
종유석의 인덱스 1은 원래 인덱스의 7과 같다. (종유석 1 == 석순 7)
따라서 코드에서

list[i]+=even[H]-even[i-1] 이 아닌, list[i]+=even[H]-even[H-i]를 해주어야 한다.
i는 석순 기준 인덱스라고 생각하면 되는데, 만약 i가 1일때 종유석의 인덱스가 7이여야 하므로 H (=7)+1-i 이 종유석의 인덱스가 되고, 거기서 -1을 해주어야 구간합을 구할 수 있기 때문에 결론적으로 H-i가 된다.
2. 자바 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static StringTokenizer st;
public static void main(String[] args) throws IOException,NumberFormatException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int H = Integer.parseInt(st.nextToken());
// 누적합 리스트
int[] odd=new int[H+1];
int[] even=new int[H+1];
for (int c = 1; c < N+1; c++) {
int curr=Integer.parseInt(br.readLine());
if(c%2!=0){
// 석순(아래에서), 홀
odd[curr]+=1;
}else {
// 종유석(위에서)
even[curr]+=1;
}
}// 입력 완료
// 누적합 구하기
for (int i = 1; i < H+1; i++) {
odd[i]=odd[i-1]+odd[i];
even[i]=even[i-1]+even[i];
}
int result2=0;
// 결과 저장할 list
int[] list=new int[H+1];
int min=Integer.MAX_VALUE;
for (int i = 1; i < H+1; i++) {
list[i]+=odd[H]-odd[i-1];
list[i]+=even[H]-even[H-i];
min=min>list[i]?list[i]:min;
}
for (int i = 1; i < H+1; i++) {
if(list[i]==min) result2++;
}
System.out.println(min+" "+result2);
}
}

누적합 문제
'알고리즘 > 백준 BOJ' 카테고리의 다른 글
| [JAVA] 백준 24513 좀비 바이러스 (0) | 2022.03.11 |
|---|---|
| [JAVA] 백준 15961,2531 회전 초밥 (0) | 2021.10.06 |
| [JAVA] 백준 1697 숨바꼭질 (0) | 2021.09.23 |
| [JAVA] 백준 21610 마법사 상어와 비바라기 (0) | 2021.09.23 |
| [JAVA] 백준 21608 상어 초등학교 (0) | 2021.09.18 |